Subsections:
Quantum Computer?A brief explanation.
Power
and Potential
Why quantum computers are special.
Related Links:
Home of the Home PagesParallel
Universes?
A debate between Deutsch and Lloyd
References:
References Below
What is a Quantum Computer?
Behold your computer. Your computer represents the culmination of years of technological advancements beginning with the early ideas of Charles Babbage (1791-1871) and eventual creation of the first computer by German engineer Konrad Zuse in 1941. Surprisingly however, the high speed modern computer sitting in front of you is fundamentally no different from its gargantuan 30 ton ancestors, which were equipped with some 18000 vacuum tubes and 500 miles of wiring! Although computers have become more compact and considerably faster in performing their task, the task remains the same: to manipulate and interpret an encoding of binary bits into a useful computational result. A bit is a fundamental unit of information, classically represented as a 0 or 1 in your digital computer. Each classical bit is physically realized through a macroscopic physical system, such as the magnetization on a hard disk or the charge on a capacitor. A document, for example, comprised of n-characters stored on the hard drive of a typical computer is accordingly described by a string of 8n zeros and ones. Herein lies a key difference between your classical computer and a quantum computer. Where a classical computer obeys the well understood laws of classical physics, a quantum computer is a device that harnesses physical phenomenon unique to quantum mechanics (especially quantum interference) to realize a fundamentally new mode of information processing.In a quantum computer, the fundamental unit of information (called a quantum bit or qubit), is not binary but rather more quaternary in nature. This qubit property arises as a direct consequence of its adherence to the laws of quantum mechanics which differ radically from the laws of classical physics. A qubit can exist not only in a state corresponding to the logical state 0 or 1 as in a classical bit, but also in states corresponding to a blend or superposition of these classical states. In other words, a qubit can exist as a zero, a one, or simultaneously as both 0 and 1, with a numerical coefficient representing the probability for each state. This may seem counterintuitive because everyday phenomenon are governed by classical physics, not quantum mechanics -- which takes over at the atomic level. This rather difficult concept is perhaps best explained through an experiment. Consider figure a below:
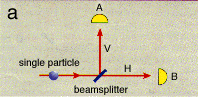 (Figure taken from a paper by Deutsch and Ekert) |
Here a light source emits a photon along a path towards a half-silvered mirror. This mirror splits the light, reflecting half vertically toward detector A and transmiting half toward detector B. A photon, however, is a single quantized packet of light and cannot be split, so it is detected with equal probability at either A or B. Intuition would say that the photon randomly leaves the mirror in either the vertical or horizontal direction. However, quantum mechanics predicts that the photon actually travels both paths simultaneously! This is more clearly demonstrated in figure b. |
In an experiment like that in figure a, where a photon is fired
at a half-silvered mirror, it can be shown that the photon does not
actually split by verifying that if one detector registers a signal, then
no other detector does. With this piece of information, one might
think that any given photon travels either vertically or horizontally,
randomly choosing between the two paths. However, quantum mechanics
predicts that the photon actually travels both paths simultaneously,
collapsing down to one path only upon measurement. This effect,
known as single-particle interference, can be better illustrated in
a slightly more elaborate experiment, outlined in figure b below:
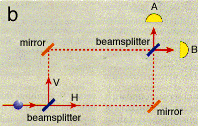 (Figure taken from a paper by Deutsch and Ekert) |
In this experiment, the photon first encounters a half-silvered mirror, then a fully silvered mirror, and finally another half-silvered mirror before reaching a detector, where each half-silvered mirror introduces the probability of the photon traveling down one path or the other. Once a photon strikes the mirror along either of the two paths after the first beam splitter, the arrangement is identical to that in figure a, and so one might hypothesize that the photon will reach either detector A or detector B with equal probability. However, experiment shows that in reality this arrangement causes detector A to register 100% of the time, and never at detector B! How can this be? |
Figure b depicts an interesting experiment that demonstrates the
phenomenon of single-particle interference. In this case, experiment
shows that the photon always reaches detector A, never
detector B! If a single photon travels vertically and strikes the
mirror, then, by comparison to the experiment in figure a, there
should be an equal probability that the photon will strike either detector
A or detector B. The same goes for a photon traveling down
the horizontal path. However, the actual result is drastically
different. The only conceivable conclusion is therefore that the
photon somehow traveled both paths simultaneously, creating an
interference at the point of intersection that destroyed the possibility
of the signal reaching B. This is known as quantum interference
and results from the superposition of the possible photon
states, or potential paths. So although only a single photon
is emitted, it appears as though an identical photon exists and travels
the 'path not taken,' only detectable by the interference it causes with
the original photon when their paths come together again. If, for
example, either of the paths are blocked with an absorbing screen, then
detector B begins registering hits again just as in the first
experiment! This unique characteristic, among others, makes the
current research in quantum computing not merely a continuation of today's
idea of a computer, but rather an entirely new branch of thought.
And it is because quantum computers harness these special characteristics
that gives them the potential to be incredibly powerful computational
devices.
The Potential and Power of Quantum Computing
In a traditional computer, information is encoded in a series of bits, and these bits are manipulated via Boolean logic gates arranged in succession to produce an end result. Similarly, a quantum computer manipulates qubits by executing a series of quantum gates, each a unitary transformation acting on a single qubit or pair of qubits. In applying these gates in succession, a quantum computer can perform a complicated unitary transformation to a set of qubits in some initial state. The qubits can then be measured, with this measurement serving as the final computational result. This similarity in calculation between a classical and quantum computer affords that in theory, a classical computer can accurately simulate a quantum computer. In other words, a classical computer would be able to do anything a quantum computer can. So why bother with quantum computers? Although a classical computer can theoretically simulate a quantum computer, it is incredibly inefficient, so much so that a classical computer is effectively incapable of performing many tasks that a quantum computer could perform with ease. The simulation of a quantum computer on a classical one is a computationally hard problem because the correlations among quantum bits are qualitatively different from correlations among classical bits, as first explained by John Bell. Take for example a system of only a few hundred qubits, this exists in a Hilbert space of dimension ~1090 that in simulation would require a classical computer to work with exponentially large matrices (to perform calculations on each individual state, which is also represented as a matrix), meaning it would take an exponentially longer time than even a primitive quantum computer.Richard Feynman was among the first to recognize the potential in quantum superposition for solving such problems much much faster. For example, a system of 500 qubits, which is impossible to simulate classically, represents a quantum superposition of as many as 2500 states. Each state would be classically equivalent to a single list of 500 1's and 0's. Any quantum operation on that system --a particular pulse of radio waves, for instance, whose action might be to execute a controlled-NOT operation on the 100th and 101st qubits-- would simultaneously operate on all 2500 states. Hence with one fell swoop, one tick of the computer clock, a quantum operation could compute not just on one machine state, as serial computers do, but on 2500 machine states at once! Eventually, however, observing the system would cause it to collapse into a single quantum state corresponding to a single answer, a single list of 500 1's and 0's, as dictated by the measurement axiom of quantum mechanics. The reason this is an exciting result is because this answer, derived from the massive quantum parallelism achieved through superposition, is the equivalent of performing the same operation on a classical super computer with ~10150 separate processors (which is of course impossible)!!
Early investigators in this field were naturally excited by the potential of such immense computing power, and soon after realizing its potential, the hunt was on to find something interesting for a quantum computer to do. Peter Shor, a research and computer scientist at AT&T's Bell Laboratories in New Jersey, provided such an application by devising the first quantum computer algorithm. Shor's algorithm harnesses the power of quantum superposition to rapidly factor very large numbers (on the order ~10200 digits and greater) in a matter of seconds. The premier application of a quantum computer capable of implementing this algorithm lies in the field of encryption, where one common (and best) encryption code, known as RSA, relies heavily on the difficulty of factoring very large composite numbers into their primes. A computer which can do this easily is naturally of great interest to numerous government agencies that use RSA -- previously considered to be "uncrackable" -- and anyone interested in electronic and financial privacy.
Encryption, however, is only one application of a quantum computer. In addition, Shor has put together a toolbox of mathematical operations that can only be performed on a quantum computer, many of which he used in his factorization algorithm. Furthermore, Feynman asserted that a quantum computer could function as a kind of simulator for quantum physics, potentially opening the doors to many discoveries in the field. Currently the power and capability of a quantum computer is primarily theoretical speculation; the advent of the first fully functional quantum computer will undoubtedly bring many new and exciting applications.
A Brief History of Quantum Computing
The idea of a computational device based on quantum mechanics was first explored in the 1970's and early 1980's by physicists and computer scientists such as Charles H. Bennett of the IBM Thomas J. Watson Research Center, Paul A. Benioff of Argonne National Laboratory in Illinois, David Deutsch of the University of Oxford, and the late Richard P. Feynman of the California Institute of Technology (Caltech). The idea emerged when scientists were pondering the fundamental limits of computation. They understood that if technology continued to abide by Moore's Law, then the continually shrinking size of circuitry packed onto silicon chips would eventually reach a point where individual elements would be no larger than a few atoms. Here a problem arose because at the atomic scale the physical laws that govern the behavior and properties of the circuit are inherently quantum mechanical in nature, not classical. This then raised the question of whether a new kind of computer could be devised based on the principles of quantum physics.Feynman was among the first to attempt to provide an answer to this question by producing an abstract model in 1982 that showed how a quantum system could be used to do computations. He also explained how such a machine would be able to act as a simulator for quantum physics. In other words, a physicist would have the ability to carry out experiments in quantum physics inside a quantum mechanical computer.
Later, in 1985, Deutsch realized that Feynman's assertion could eventually lead to a general purpose quantum computer and published a crucial theoretical paper showing that any physical process, in principle, could be modeled perfectly by a quantum computer. Thus, a quantum computer would have capabilities far beyond those of any traditional classical computer. After Deutsch published this paper, the search began to find interesting applications for such a machine.
Unfortunately, all that could be found were a few rather contrived mathematical problems, until Shor circulated in 1994 a preprint of a paper in which he set out a method for using quantum computers to crack an important problem in number theory, namely factorization. He showed how an ensemble of mathematical operations, designed specifically for a quantum computer, could be organized to enable a such a machine to factor huge numbers extremely rapidly, much faster than is possible on conventional computers. With this breakthrough, quantum computing transformed from a mere academic curiosity directly into a national and world interest.
Obstacles and Research
The field of quantum information processing has made numerous promising advancements since its conception, including the building of two- and three-qubit quantum computers capable of some simple arithmetic and data sorting. However, a few potentially large obstacles still remain that prevent us from "just building one," or more precisely, building a quantum computer that can rival today's modern digital computer. Among these difficulties, error correction, decoherence, and hardware architecture are probably the most formidable. Error correction is rather self explanatory, but what errors need correction? The answer is primarily those errors that arise as a direct result of decoherence, or the tendency of a quantum computer to decay from a given quantum state into an incoherent state as it interacts, or entangles, with the state of the environment. These interactions between the environment and qubits are unavoidable, and induce the breakdown of information stored in the quantum computer, and thus errors in computation. Before any quantum computer will be capable of solving hard problems, research must devise a way to maintain decoherence and other potential sources of error at an acceptable level. Thanks to the theory (and now reality) of quantum error correction, first proposed in 1995 and continually developed since, small scale quantum computers have been built and the prospects of large quantum computers are looking up. Probably the most important idea in this field is the application of error correction in phase coherence as a means to extract information and reduce error in a quantum system without actually measuring that system. In 1998, researches at Los Alamos National Laboratory and MIT led by Raymond Laflamme managed to spread a single bit of quantum information (qubit) across three nuclear spins in each molecule of a liquid solution of alanine or trichloroethylene molecules. They accomplished this using the techniques of nuclear magnetic resonance (NMR). This experiment is significant because spreading out the information actually made it harder to corrupt. Quantum mechanics tells us that directly measuring the state of a qubit invariably destroys the superposition of states in which it exists, forcing it to become either a 0 or 1. The technique of spreading out the information allows researchers to utilize the property of entanglement to study the interactions between states as an indirect method for analyzing the quantum information. Rather than a direct measurement, the group compared the spins to see if any new differences arose between them without learning the information itself. This technique gave them the ability to detect and fix errors in a qubit's phase coherence, and thus maintain a higher level of coherence in the quantum system. This milestone has provided argument against skeptics, and hope for believers. Currently, research in quantum error correction continues with groups at Caltech (Preskill, Kimble), Microsoft, Los Alamos, and elsewhere.At this point, only a few of the benefits of quantum computation and quantum computers are readily obvious, but before more possibilities are uncovered theory must be put to the test. In order to do this, devices capable of quantum computation must be constructed. Quantum computing hardware is, however, still in its infancy. As a result of several significant experiments, nuclear magnetic resonance (NMR) has become the most popular component in quantum hardware architecture. Only within the past year, a group from Los Alamos National Laboratory and MIT constructed the first experimental demonstrations of a quantum computer using nuclear magnetic resonance (NMR) technology. Currently, research is underway to discover methods for battling the destructive effects of decoherence, to develop an optimal hardware architecture for designing and building a quantum computer, and to further uncover quantum algorithms to utilize the immense computing power available in these devices. Naturally this pursuit is intimately related to quantum error correction codes and quantum algorithms, so a number of groups are doing simultaneous research in a number of these fields. To date, designs have involved ion traps, cavity quantum electrodynamics (QED), and NMR. Though these devices have had mild success in performing interesting experiments, the technologies each have serious limitations. Ion trap computers are limited in speed by the vibration frequency of the modes in the trap. NMR devices have an exponential attenuation of signal to noise as the number of qubits in a system increases. Cavity QED is slightly more promising; however, it still has only been demonstrated with a few qubits. Seth Lloyd of MIT is currently a prominent researcher in quantum hardware. The future of quantum computer hardware architecture is likely to be very different from what we know today; however, the current research has helped to provide insight as to what obstacles the future will hold for these devices.
Future Outlook
At present, quantum computers and quantum information technology remains in its pioneering stage. At this very moment obstacles are being surmounted that will provide the knowledge needed to thrust quantum computers up to their rightful position as the fastest computational machines in existence. Error correction has made promising progress to date, nearing a point now where we may have the tools required to build a computer robust enough to adequately withstand the effects of decoherence. Quantum hardware, on the other hand, remains an emerging field, but the work done thus far suggests that it will only be a matter time before we have devices large enough to test Shor's and other quantum algorithms. Thereby, quantum computers will emerge as the superior computational devices at the very least, and perhaps one day make today's modern computer obsolete. Quantum computation has its origins in highly specialized fields of theoretical physics, but its future undoubtedly lies in the profound effect it will have on the lives of all mankind.References:
1. D. Deutsch, Proc. Roy. Soc. London, Ser. A 400, 97 (1985).2. R. P. Feynman, Int. J. Theor. Phys. 21, 467 (1982).
3. J. Preskill, "Battling Decoherence: The Fault-Tolerant Quantum Computer," Physics Today, June (1999).
4. Shor, P. W., Algorithms for quantum computation: Discrete logarithms and factoring, in Proceedings of the 35th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press (1994).
5. Nielsen, M., "Quantum Computing," (unpublished notes) (1999).
6. QUIC on-line, "Decoherence and Error Correction," (1997).
7. D.G. Cory et al., Physical Review Letters, 7 Sept 1998.
8. J. Preskill, "Quantum Computing: Pro and Con," quant-ph/9705032 v3, 26 Aug 1997.
9. Chuang, I. L., Laflamme, R., Yamamoto, Y., "Decoherence and a Simple Quantum Computer," (1995).
10. D. Deutsch, A. Ekert, "Quantum Computation," Physics World, March (1998).